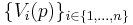Parallelizable manifold

In mathematics, a parallelizable manifold 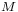$\scriptstyle M$ ^[1] is a smooth manifold of dimension n having vector fields

$\{V_1, \dots,V_n\}$

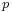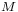such that at any point $\scriptstyle p$ of $\scriptstyle M$ the tangent vectors

$\{V_i(p)\}_{i\in \{1,\dots,n\}}$

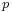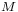provide a basis of the tangent space at $\scriptstyle p$ . Equivalently, the tangent bundle is a trivial bundle,^[2] so that the associated principal bundle of linear frames has a section on $\scriptstyle M$ .

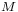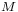A particular choice of such a basis of vector fields on $\scriptstyle M$ is called a parallelization (or an absolute parallelism) of $\scriptstyle M$ .

1 Examples
2 Remarks
3 See also
4 Notes
5 References

Examples

An example with n = 1 is the circle: we can take V₁ to be the unit tangent vector field, say pointing in the anti-clockwise direction. The torus of dimension n is also parallelizable, as can be seen by expressing it as a cartesian product of circles. For example, take n = 2, and construct a torus from a square of graph paper with opposite edges glued together, to get an idea of the two tangent directions at each point. More generally, any Lie group G is parallelizable, since a basis for the tangent space at the identity element can be moved around by the action of the translation group of G on G (any translation is a diffeomorphism and therefore these translations induce linear isomorphisms between tangent spaces of points in G).

A classical problem was to determine which of the spheres Sⁿ are parallelizable. The case S¹ is the circle, which is parallelizable as has already been explained. The hairy ball theorem shows that S² is not parallelizable. However S³ is parallelizable, since it is the Lie group SU(2). The only other parallelizable sphere is S⁷; this was proved in 1958, by Michel Kervaire, and by Raoul Bott and John Milnor, in independent work.

Every Lie group is a parallelizable manifold.

The product of parallelizable manifolds is parallelizable.

Remarks

The term framed manifold (occasionally rigged manifold) is most usually applied to an embedded manifold with a given trivialisation of the normal bundle, and also for an abstract (i.e. non-embedded) manifold with a given stable trivialisation of the tangent bundle.

Notes

^ Bishop, R.L.; Goldberg, S.I. (1968), p. 160
^ Milnor, J.W.; Stasheff, J.D. (1974), p. 15

References

Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds (First Dover 1980 ed.), The Macmillan Company, ISBN 0-486-64039-6
Milnor, J.W.; Stasheff, J.D. (1974), Characteristic Classes, Princeton University Press

Parallelizable manifold

Contents

Examples

Remarks

See also

Notes

References